松島研究室では、データ理解のための機械学習基盤の研究を行っています。

現在の社会では、都市のインフラや地球環境に関するデータ、医療・健康関連データ、マーケティングデータ、材料・物性に関するデータなど多種多様なデータが日々生成されています。現在ではこれらの大規模データを機械学習技術を用いて分析・活用することは、新たな社会システムやサービスを生み出す情報基盤技術の発展に不可欠です。
大規模データのための最適化アルゴリズムは機械学習の基礎理論「統計的学習理論」と、実践的応用の「データマイニング」の両輪を支える軸であるといえます。本研究室では、データから得られる分析結果を知識として表現することで複雑なデータの全体像を理解するための機械学習技術の確立と、そのための最適化アルゴリズムの研究開発を行っています。
データ理解のための機械学習
機械学習が関わるデータ分析は、タスク志向型とデータ駆動型の2つに大別されます。
タスク志向型では、解決すべきタスクに基づいてデータを収集・整形し予測器を学習します。一方のデータ駆動型分析は、複雑なデータの全体像を把握し、知識を発見・可視化するために予測器を学習します。当研究室ではデータ駆動型機械学習に着目し、交通データやウェブマーケティングデータを用いたデータの理解に関する研究に取り組んでいます。
例えば交通データを理解するといったとき、ある道路が他の道路に比べてなぜ自転車事故が多いのか?という説明ができること、その道路に自転車専用レーンを設置した場合の自転車事故の変化が予測できること、これらがデータの理解を形成する知識の二つの要素と考えます。すなわち、データの学習結果に対し比較に基づく説明を可能にすることと、分析者の行動に対する系の応答が予測できることが特に重要であるといえます。そのような考え方に基づき、データに関する説明を与えることができるモデルとして解釈可能な予測モデルの研究とデータへの介入を行ったときの挙動の予測を与えることができるモデルとして因果モデルの研究を行っています。
解釈可能な予測モデル
機械学習を用いて何らかのデータからターゲットを予測する予測関数を得たいというときは、その予測関数に分析者が理解するための解釈を与えたいという場合が多いです。一方、機械学習によって学習される予測関数は、(深層学習を用いる場合など)多くの場合で非常に複雑な関数を用いています。そのため、高い精度で予測できる関数を手に入れられたとて、予測関数をどのように解釈すればよいか?という問題が残ることがあります。
近年では機械学習において解釈可能性は一つのキーワードとなっており、「関数を解釈するというのはどのようなことか?」という根本的な議論をはじめとしてモデルの解釈可能性に関する議論が活発に行われています。一つの考え方として、予測関数fと予測関数への入力xを与えたときに説明eを返す関数がfとxの解釈器と考えることができます。説明は典型的には「なぜ予測関数fは入力xに対してf(x)という予測をするのか」を表しますが、他にも様々な形の説明があり得ます。そして、どんな入力に関しても自然に特定の形の説明を返す解釈器を持つような関数のみを集めたモデルが解釈可能なモデルということです。
松島研究室では、解釈可能な予測モデルとして一般化加法モデル[1]や組合せ二変数モデル[2]に着目し、これらの効率的な学習手法の確立を目指しています。これらのモデルはモデルの複雑性は高い一方で、データが本質的に複雑でなければ、学習される予測関数自体は解釈可能な単純なものになることが期待されます。現在までの研究でこれらの手法の学習は座標降下法をベースにした最適化アルゴリズムが有効であることが示されていますが、さらに効率の良いアルゴリズムや、これらを活かしたさらに解釈性の高いモデルなどの開発を目指しています。
[1] Hastie, T. J. (2017). Generalized additive models. Routledge.
[2] Lee, T., Matsushima, S., & Yamanishi, K. (2020). Grafting for combinatorial binary model using frequent itemset mining. Data Mining and Knowledge Discovery, 34(1), 101-123.
因果探索への情報理論的アプローチ
統計的な推論の大前提として、データのすべての性質は(場合によっては潜在変数もふくめた)データの分布により記述することができるというものがあります。「与えられたデータを用いて真の同時分布を推定することで、データの生成過程について知ることができる」という考え方はこのような前提に基づいているといえます。一方で、例えばウェブマーケティングデータの分析者がユーザに特定のページを表示させることができる場合など、データの生成過程に関して一定の介入をすることができる場合も多いです。そのような場合は、データ生成過程に関して介入できる部分と介入できない部分を切り分けられるように前提を立て直して、分析者の介入に依らない不変の構造を知ることが問題となります。
近年では機械学習の文脈でも統計的因果探索あるいは統計的因果推論というキーワードとともにこのような議論が活発に議論されています。データの生成過程の中でも分析者が介入できない部分を「因果構造 (causal structure)」あるいは「因果機構(causal mechanism)」などとよび、これらを様々なデータや統計的な道具を使うことで調べる方法が提案されてきています。例えば、統計的な意味での独立性を超えて因果機構の算法的な独立性を調べるために情報理論に基づく符号化の方法を利用する方法などが知られてます[3]。
松島研究室では、情報理論的なモデル選択がデータの因果機構の特定に有効であるという考え方に基づき、データから因果機構を推定する手法の確立を目指しています。現在までの研究によって統計的因果探索には情報論的なアプローチが有効であることが知られています。我々は、変数の数が非常に少ない場合では情報論的モデル選択がデータ生成機構の推定に有効であることを示しましたが、さらに複雑なデータ・大規模なデータに対する因果探索手法の開発を目指しています[4]。
[3] Schölkopf, B. (2022). Causality for machine learning. In Probabilistic and Causal Inference: The Works of Judea Pearl (pp. 765-804).
[4] Kobayashi, M., Miyaguchi, K., & Matsushima, S. (2022). Detection of Unobserved Common Cause in Discrete Data Based on the MDL Principle. In IEEE International Conference on Big Data (pp. 45-54).
現在の研究
学習基盤の研究
機械学習の最適化を図るアルゴリズムの研究開発を行っています。
Dual Cached Loops
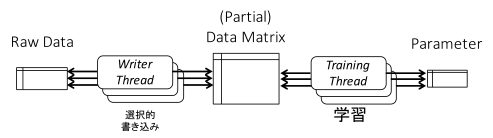
Dual Cached Loops(DCL)は、2つのスレッドを非同期的に動作させることで機械学習の最適化を図るアルゴリズムです。Writer thread とよばれるスレッドはハードディスクに連続アクセスし、繰り返しデータをRAMへ読み込みます。一方の Training Thread とよばれるスレッドは、高速かつ継続的にパラメータを更新します。これを用いることで、メモリ容量を超えるデータの高速な処理が可能になり、テラバイトスケールの問題を単一のマシンで学習できることを明らかにしました。
同時分解性を用いた分散最適化
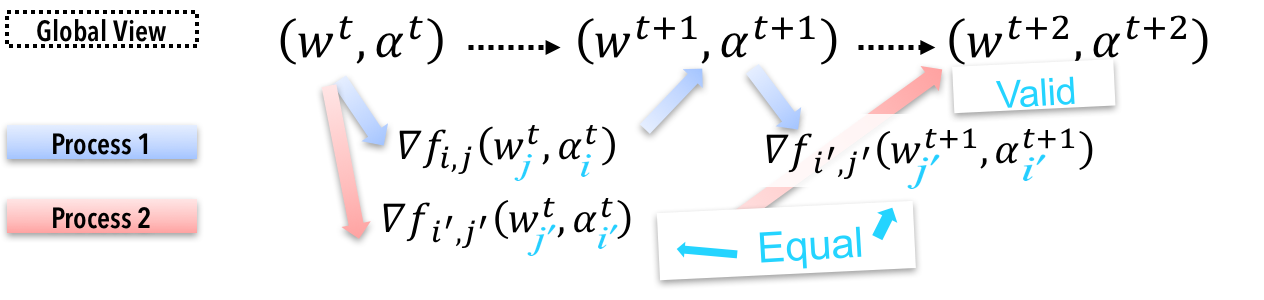
知識発見の際にも現れる正則化つき経験リスク最小化問題において、単一マシンでは扱うことができないほど大規模なデータを分散環境で扱う場合、確率的最適化法が多く利用されます。確率的最適化法を分散環境で行う場合、パラメータを頻繁に同期させる必要があり、これが計算時間のボトルネックになっています。
Distributed Stochastic Optimization(DSO)では経験リスク最小化問題と同値な鞍点問題を扱うことにより、パラメータの同期を軽減させる手法を確立しました。
過去の卒業研究
「二変数間の相互作用を考慮した一般化加法モデルとその効率的な学習」
「半順序集合上の対数線形モデルのための座標降下法」
「数理最適化の観点から行うDirect LiNGAMの改善アルゴリズムの提案」
多くの科学の分野では、起きている現象の背後にある因果構造を把握することを目的にして実験や研究がおこなわれることが多いです。因果構造を正確に把握するためには介入を行った際に得られるデータが必要となりますが、そのようなデータが得られることは稀で、通常は観測データのみから因果構造を推定する必要があります。
その推定に関する既存手法のうちのLiNGAMの1つのアプローチであるShimizu et al. (2011)のDirect LiNGAMに対して、数理最適化を活用することで因果推論を行うZheng et al. (2018)によるNO TEARSと同様に、グラフに関する特殊な知識を要しないような目的関数の定式化を行い、その目的関数に対して厳密な最適化を行うことで、従来のDirect LiNGAMの精度を上回ることを示しました。
「半順序集合上の対数線形モデルのための加速座標降下法」
半順序集合上の対数線形モデルは, 対数線形モデルのデータ空間を線形空間から半順序集合に拡張させた離散確率モデルである. このモデルの利点は, 高次元の交互作用項も考慮できること, 様々な有名なモデルを包含することが挙げられる. しかし, 最適化アルゴリズムを単純に適用した場合, 1イタレーションが半順序集合の要素数に比例し莫大な計算量を必要となる. 先行研究では, この問題を回避し, 反復計算量がO(ε^{-1})となるアルゴリズムを提案した。本研究では, この問題を回避しつつO(ε^{-0.5})となる加速座標降下法を提案した.
